autori: Prof.dr.sc. Darko Stipaničev, dr.sc. Ljiljana Šerić, Marin Bugarić, dipl.ing.- Fakultet elektrotehnike, strojarstva i brodogradnje Sveučilišta u Splitu
Modeli matematičkih analogija su oni koji koriste matematičke zakone, a ne fizikalne zakone kod modeliranja širenja vatre, a simulacijski modeli su oni koji koriste bilo koju grupu prethodnih modela sa ciljem simulacije širenja šumskog požara najčešće u dvo-dimenzionalnom prostoru.
Modeli matematičkih analogija
Postoji veliki broj radova koji širenje požara nastoje modelirati matematičkim analogijama. Nastoji se pronaći matematički postupak koji daje rezultate analogne stvarnom širenju vatre. U ovu grupu spadaju celularni automati, samo-organizirani sustavi kritičnog ponašanja, jednadžbe reakcije – difuzije, perkolacijski modeli, neuralne mreže i slično.
Celularni automati i samo-organizirajući sustavi kritičnog ponašanja
Celularni automati (eng CA – Celluar Automata) koji se ponekad zovu i stanični automati ili ćelijski automati model su fizikalnog sustava diskretiziranog i po prostoru i po vremenu. Sastoje se od pravilne n-dimezionalne rešetke čija su polja stanice (ćelije, celule). Svaka od stanica može biti u jednom od konačnog broja mogućih stanja, a stanje pojedine stanice se mijenja u diskretnim vremenskim intervalima ovisno o stanju susjednih stanica.
Vegetacija otvorenog prostora se može promatrati kao dvo-dimenzionalni celularni automat. Svaka stanica predstavlja fiksnu površinu koja odgovarajuće atribute koje ogovaraju svojstvima okoliša, prije svega svojstvima vegetacijskog pokrova u odnosu na gorivost i svojstvima topografskih karakteristika terena.
Predloženo je više različitih modela simulacije širenja šumskog požara pomoću celularnih automata [Lj.Bodrožić, J.Marasović, D.Stipaničev, Fire Modelling in Forest Fire management, Proc.of Int. Conf. CEEPUS Spring School – Engineering for the Future, Kielce, Poland 6-16.06.2005. pp. 7 – 15, Lj.Bodrožić, D.Stipaničev, M.Šerić, Forest Fires Spread Modeling Using Cellular Automata Approach, Proc.of Int. Conf. CEEPUS Summer School – Modern trends in control, Košice, Slovak Republic, 1-15.7.2006. pp. 23-33], a najčešće se celularni automati kombiniraju sa Rothermelovim modelom za proračun parametara gorenja o čemu ćemo više kazati u Poglavlju 2.3.3.2. Ovdje ćemo spomenuti samo to da početak požara (zapaljenje) može biti vezan s jednom ili više početnih stanica, a svaka od stanica može se nalaziti u jednom od 4 moguća stanja:
• stanje 1 – stanica ne gori
• stanje 2 – stanica kroz koju se požar ne može propagirati
• stanje 3 – stanica kroz koju se požar može propagirati
• stanje 4 – stanica gori
Najveći problem u modeliranju širenja požara celularnim automatima je definiranje veze između vremenskih koraka modela i stvarnog vremena. Kada se stanica zapali, ona iz stanja 1 prelazi u stanje 2, a stanica koja je već u stanju 4 ostaje u tom stanju. Broj vremenskih koraka je s toga važan samo za stanice u stanju 2 i 3. Za svaku interakciju unutar modela bitne su stanice propagacije i njihovo susjedstvo od osam susjednih stanica.
Razvijeni su modeli širenja požara u izotropnim uvjetima kada širenje požara ovisi samo o neposrednom susjedstvu i kada se uzima u obzir utjecaj vjetra i padine, ali i u anizotropnim uvjetima kada se uzima u obzir i vjetar i padina, ali i širenje požara po prizemnom sloju goriva i po krošnjama .
Općenitija teorija koja među ostalim kod modeliranja koristi i celularne automate je teorija samo-organizirajućih sustava kritičnog ponašanja. Samo-organizirajući sustavi kritičnog ponašanja, poznati u literaturi kao SOC (Self-Organised Criticality) modeli, otkriće su statističke fizike u drugoj polovici XX stoljeća tijekom izučavanja problema kompleksnosti prirode. Šumski požari, lavine i potresi neki su od prvih modela kojima je ilustrirana teorija samo-organizirajući sustavi kritičnog ponašanja. Primjenom na ove pojave nastojalo se pokazati da dinamički sustavi sa prostornim stupnjevima slobode evoluiraju u kritično samo-organizirajuće stanje koje je invarijantno na skaliranje i robustno na perturbacije.
Perkolacijski modeli
Perkolacija je u kemiji i znanosti o materijalima proces transporta fluida kroz porozni materijal, a u matematici teorija koncentrirana na prijenos kroz slučajno distribuirani medij [Sullivan, A.L. A review of wildland fire spread modelling, 1990-2007, 3: Simulation and mathematical analogue models, International Journal of Wildland Fire, 18, 387-403, K.Biljaković (mentor), A.Kis, D.Bonacci, A.Colovic, Simulacija šumskih požara, E-škola, http://eskola.hfd.hr/mini_projekt/mp3/mp3.htm ]. Ukoliko je medij regularna latica, perkolacija se može smatrati općim slučajem izotropnih celularnih automata.
Perkolaciju najjednostavnije možemo objasniti na primjeru dvodimenzionalne rešetke koji prenosimo iz [K.Biljaković (mentor), A.Kis, D.Bonacci, A.Colovic, Simulacija šumskih požara, E-škola, http://eskola.hfd.hr/mini_projekt/mp3/mp3.htm ]:
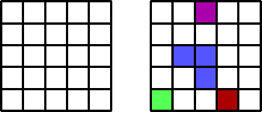
'' Pretpostavimo jednostavnu dvo-dimenzionalnu rešetku kao na slici. Neka je svako polje popunjeno s vjerojatnošću p, neovisno o popunjenosti susjednih polja. Popunjena polja koja su jedna drugima najbliži susjedi (imaju jednu zajednički stranicu) nazivaju se grozdovima. Tako na desnoj strani slike, polja koja su označena istom bojom pripadaju zajedničkom grozdu. Kako povećavamo vjerojatnosti p, može se u sistemu pojaviti grozd koji se prostire s jednog kraja na drugi - perkolirajući grozd. Granična vjerojatnost na kojoj dolazi do pojave ovakvog grozda naziva se vjerojatnost praga i označava s pc . To je vjerojatnost na kojoj se prvi put formira perkolirajući grozd. Za 2D kvadratičnu rešetku se dobiva pc = 0.59. Gornja matrica i popunjena polja mogu predstavljati različite sisteme.
Kod perkolacijskih modela širenja požara šuma se pojednostavljeno prikazuje kao dvo-dimenzionalna pravokutna rešetka. Svako polje može biti u jednom od tri stanja:
- ne gori (zeleno polje),
- gori (crveno polje) i
- izgorjelo (crno polje).
Za svaka se polja definira i prijelazna vjerojatnost preskoka vatre s tog polja na okolna polja. Da bismo vidjeli kako se vatra širi, moramo prvo odrediti kriterije po kojem će se paliti pojedina polja. U prvom slučaju možemo uzeti da je zeleno polje postalo crveno (vegetacija se zapalila) ako postoji susjedno crveno polje. Prilikom simuliranja krećemo od linije zapaljenja u kojoj su sva polja crvena. Zatim prelazimo po matrici prostora liniju po liniju i pretvaramo zelena polja u crvena po danom kriteriju. Kad dođemo do zadnje linije ponavljamo postupak. Svaki ovakav prijelaz po matrici predstavlja jedan vremenski korak simulacije. Pretpostavit ćemo pojednostavljeno da u svakom ciklusu crvena polja, nakon što su zapalila svoje susjede postaju crna polja (hrpa pepela), koja više ne gore i ne pale okolna polja. Vrijeme trajanja požara je broj vremenskih koraka u simulaciji. U ovakav model se preko kriterija za širenje požara mogu uvesti i vremenske prilike. Može se uvest kriterij da po vrućem vremenu drvo koje gori može zapaliti ne samo najbliže, već i slijedeće najbliže susjede (to su ona polja koja imaju zajedničke vrhove). Za slučaj vlažnog vremena uvjet da bi se polje zapalilo može biti da u susjedstvu mora imati dva goruća polja. Pojavi perkolacije u ovom modelu odgovara širenje požara kroz cijelu šumu.''
Reakcija - difuzija
Reakcija – difuzija je u kemiji pojam koji opisuje proces u kojemu dvije ili više kemikalija difuzijom prodiru na odgovarajuću površinu reagirajući pri tom ukoliko jedna s drugom dođu u kontakt. Reakcija interferencije difuznih komponenata najčešće formira frontu koja se kreže kroz površinu reakcije, a može se opisati valnim jednadžbama. Jednadžbe reakcije – difuzije se smatraju jednim od najopćenitijih jednadžbi i mogu se primijeniti u opisivanju cijelog niza različitih fenomena. Imaju dva dijela:
- reakcijski dio koji proizvodi energiju i
- difuzijski dio koji troši energiju.
Matematički reakcijsko – difuzijsku jednadžbu izražavamo semi-linearnom paraboličnom parcijalnom diferencijalnom jednadžbom:
∂q/∂t = D Δq + R(q)
gdje je:
q(x,t) – koncentracija jedne substance,
D - dijagonalna matrica difuzijskih koeficijenata, a
R su lokalne reakcije
Opće rješenje reakcijsko – difuzijskih jednadžbi može dati formiranje propagacijskog vala, ali i različite oblike samo-organizirajućih struktura.
Reakcijsko – difuzijske jednadžbe su pretežno na razini istraživanja korištene za simulaciju šumskih požara i to pogotovo u drugoj polovici 90-ih godina prošlog stoljeća, međutim koliko je nama poznato do danas ovaj postupak nije korišten u praktičnoj izvedbi simulatora požara pa ga dalje niti ne izučavamo.