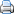autori: Prof.dr.sc. Darko Stipaničev, dr.sc. Ljiljana Šerić, Marin Bugarić, dipl.ing.- Fakultet elektrotehnike, strojarstva i brodogradnje Sveučilišta u Splitu
Fizikalni modeli su oni koji se temelje na fizikalnim i kemijskim zakonima vezanim uz širenje vatre, dok se kvazi-fizikalni naslanjaju isključivo na fizikalne opise širenja. Grishin [Grishin, A., Mathematical Modelling of forest fires and new methods of fighting them, Publishing House of Tomsk State University, Tomsk, Russia, english translation edition. Translated from Russianby Marek Czuma, L Chikina and L Smokotina.] autor jednog od modela ističe 5 koraka u razvoju determinističkog modela:
- Fizikalna analiza fenomena požara raslinja: izoliranje mehanizama koji vode prijenos energije sa vatrene fronte na okoliš, definiranje tipa medija i kreiranje fizikalnog modela fenomena.
- Određivanje reakcijskih i termo-fizikalnih svojstava medija, koeficijenata prijenosa i strukturnih parametara medija, izvođenje osnovnih jednadžbi i odgovarajućih graničnih i početnih uvjeta.
- Odabir postupka numeričkog rješavanja problema, izvođenje diferencijalnih jednadžbi kojima se aproksimiraju osnovne jednadžbe sustava.
- Programiranje, provjera programa, procjena točnosti, numeričko rješavanje jednadžbi.
- Testiranje sa ciljem provjere koliko se dobro dobiveni rezultati poklapaju sa stvarnim podacima, fizikalna interpretacija rezultata, donošenje prijedloga i preporuka vezanih uz postupke gašenja požara koji se simulira.
Fizikalni modeli uzimaju u obzir jedan ili više procesa prijenosa energije iz goruće zone u negoruće gorivo. Opisuju kako se, zagrijavanjem nezapaljenog gorivo dio energije oslobađa na temelju čega dolazi do širenja požara. Pojednostavljeno gledajući širenje vatre je prijelaz stanja gorivih ćelija iz negorućeg u goruće pri čemu ovim prijelazom upravlja prijenos energije. Tri su glavna elementa:
- Izvor topline (predajnik toplinske energije).
- Prijenos topline.
- Prijamnik topline (apsorber toplinske energije), a čini ga nezapaljeno gorivo u okolini zapaljenog goriva.
Izvor topline oslobađa kao rezultat izgaranja specifična količina energije po jedinici površine koja ovisi o:
- Veličini svake čestice – manje čestica imaju veću površinu te otpuštaju više topline.
- Gustoći goriva.
- Količini vlage u gorivu.
- Kemijskom sastavu goriva.
Prijenos topline je proces na koji utječe puno utjecajnih faktora, teško je detaljno predvidiv a podložan je i varijacijama, pa često kod modeliranja zahtjeva velik broj pretpostavki. Različiti modeli prihvaćaju različite vrste prijenosa topline, koja se kao što smo već kazali provodi kroz tri mehanizma:
- Radijaciju - isijavanje, zračenje, prenošenje topline u obliku elektromagnetskih valova u infra-crvenom području (od 0.75 do 1000 μm valne duljine). Ovo je osnovni mehanizam prijenosa topline u požarima raslinja, pa ga uključuje većina modela.
- Kondukciju – vođenje, provođenje, vezano je obično uz provođenje topline kroz kruta tijela. Obično se zanemaruje kod modeliranja požara raslinja, jer je šumsko gorivo porozno i drvenasto, a drveni materijali loše provode toplinu.
- Konvekciju – prenošenje topline, glavni je mehanizam prijenosa topline u plinovima i kapljevinama zbog njihovog strujanja, a razlikuje se prirodna i prisilna konvekcija. Ovaj je mehanizam prijenosa topline važna za vrste vatre kod kojih se otpuštaju velike količine energije sa goruće materija u okolni zrak. Tipičan su primjer požari krošnji (krunske vatre).
Prijamnik topline. Primljena toplinska energije troši se u isušivanje goriva i zagrijavanje do temperature pirolize, a dio se gubi u obliku gubitaka na zagrijavanje okolnih medija. Količina apsorbirane topline uglavnom ovisi o:
- toplini pred-zagrijavanja i
- efektivnoj gustoći volumena goriva.
Ostale karakteristične veličine o kojima ovisi kapacitet apsorpcije topline su:
- Specifična toplina goriva i njena temperaturna ovisnost.
- Specifična toplina i entalpija isparavanja.
- Entalpija pirolize i produkata isparavanja.
- Specifična toplina pougljenih ostataka
Omjer toka napredovanja (eng. Propagating Flux Rratio) još je jedna bitna veličina koja karakterizira vatrenu frontu. Predstavlja udio ukupne brzine otpuštanja topline koji se prenosi i upija od gorivog materijala ispred vatrene fronte, te uzrokuje povećavanje njene temperature do točke zapaljenja. Vatrena fronta se obično definira kao ravna linija okomita na smjer širenja vatre.
Fizikalni modeli predstavljaju veće ili manje pojednostavljenje fizikalnih pojave vezanih uz širenje požarne fronte. Pri tome se često plamen smatra površinom fiksne temperature koji predaje energiju okolnoj vegetaciji radijacijom. Površina koja razdvaja goruću zonu od nezapaljenog goriva zove se prijelazna zona zapaljenja (eng. Ignition Interface). Fizikalni modeli širenja požara međusobno se razlikuju u odabiru kontrolnog volumena za koji se postavlja jednadžba održanja energije, te po uključivanju različitih mehanizama prijenosa energije. Kod složenijih modela uzimaju se u obzir različiti načini prijenosa energije koje ćemo kasnije detaljnije spomenuti.
Fenomen širenja požara raslinja je vrlo kompleksan. Sve pojave koje se javljaju su međusobno isprepletene i nelinearne. Iako se pojava u osnovi temelji na osnovnim zakonima održanja (energije, mase i momenta) koji su dobro poznati, problem modeliranja je u nepoznavanju nekih od fizikalnih parametara i velikoj osjetljivosti na početne i rubne uvjete, te je u osnovi vrlo teško, a slobodno bi mogli kazati skoro pa nemoguće numerički pouzdano predvidjeti razvoj požara raslinja tijekom dužeg vremenskog perioda. Fizikalno modeliranje širenja vatre na otvorenom prostoru još je uvijek izazovan problem u domeni tzv. HCP (High Performance Computing) područja [Morvan, D. Physical Phenomena in Wildfire Modelling, Modeling, Monitoring and Management of Forest Fires, J.de la Hares, C.A.Brebbia, D.Viegas, V.Leone (ed), Proc. of First Int.Conf. Forest Fires 2008, Toledo, Spain, Oct.2008. WIT Press, 2008. pp.203-212]. Iako postoje vrlo dobro razvijeni i razrađeni fizikalni modeli primjerice FLUENT koji se vrlo uspješno primjenjuju u simulaciji širenja požara zatvorenog prostora, upitna je njihova primjenjivost u simulaciji širenja požara otvorenog prostora. Kod zatvorenog prostora rubni uvjeti su dobro definirani, a kod otvorenog prostora u principu mogu se namjestiti tako da dobijete što vam odgovara.
Upravo zbog toga u praksi se puno veći značaj daje empirijskim, a pogotovo semi-empirijskim modelima, međutim zbog cjelovitosti ovdje ih navodimo. Fizikalni modeli mogu biti jednodimenzionalni (1D), dvo-dimenzionalni (2D) ili trodimenzionalni (3D).
Kod fizikalnih modela koriste se znanja iz kemije procesa gorenja i fizike procesa gorenja. Kemija gorenja raslinja otvorenog prostora kompleksan je problem, s jedne strane zbog kompliciranog i heterogenog goriva (prirodne vegetacije), ali i zbog uvjeta u kojem se gorenje događa što utječe na razvoj procesa gorenja.
Kemija gorenja uključuje:
• kemiju goriva,
• reakcije potrebne da bi gorenje počelo,
• reakcije gorenja čvrste faze (toplinska degradacija), i
• reakcije gorenja plinovite faze
U svim slučajevima zbog specifičnosti vegetacije otvorenog prostora i okolnosti u kojima se gorenje odvija radi se o kompleksnim pojavama koje je vrlo teško u potpunosti obuhvatiti i sagledati, pa se najčešće uvode brojna pojednostavljenja.
Fizike gorenja je po kompleksnosti problema slična kemiji gorenja, a poseban problem čine promjenjivi uvjeti u kojima do gorenja dolazi. Osnovni fizikalni proces kod požara otvorenog prostora je prijenos topline, i to na više načina. Spominje se mogući prijenos topline:
1. difuzija radikala,
2. prijenos topline kondukcijom kroz plinove,
3. prijenos topline kondukcijom kroz sabijenu materiju,
4. prijenos topline konvekcijom kroz plinove,
5. radijacija žara,
6. radijacija plamena,
7. radijacija negorućih čestica,
8. prijenos topline preskakanjem čestica krutog zapaljenog goriva iz zapaljenog dijela u nezapaljeni dio, najčešće uz pomoć vjetra (eng. spottingt).
Mehanizmi 1, 2 i 3 obično se klasificiraju kao difuzija na molekularnoj razini, 4 je klasična konvekcija topline plinovima, 5, 6 i 7 su različiti oblici prijenosa topline radijacijom, a 8 je prijenos topline preko krute tvari specifičan za požare otvorenog prostora, kada čestice zapaljenog goriva i žara nošene vjetrom dolaze do nezapaljenih područja i uzrokuju nova zapaljenja. Ovaj posljednji mehanizam posebno je prisutan kod gorenja borovih šuma. Tome se trebaju dodati i pred-ugrijavanje goriva, te različiti gubici energije, pa se modeli često i razlikuju po tome koje od ovih mehanizama uzimaju u obzir.
Temeljna pretpostavka kod više-manje manje svih fizikalnih modela širenja vatre je ta da se gibanje četica plinova nastalih kao produkt izgaranja smatra fluidom, a gibanje kontinuirano gibanje fluida, a ne gibanje kolektiviteta čestica. Zbog toga su zakoni širenja požara raslinja u osnovi temelje na dobro poznatoj dinamici fluida i jednadžbama održanja mase, momenta i energije [Sullivan, A.L. A review of wildland fire spread modelling, 1990-2007, 1: Physical and quasi-physical models, Journal of Wildland Fire 18, 349-368].
Jednadžba održanja mase: povezuje brzinu fluida, gustoću i vrijeme:
∂ρ/∂ t + ∇(ρu) = 0
ρ je gustoća, t vrijeme, u brzina fluida (vektorski izražena s komponentama u, v i w) i ∇ Laplaceov gradijentni operator (i ∂/∂x + j ∂/∂x + k ∂/∂x). Rješenje jednadžbe zahtijeva poznavanje razvoja brzine u. Ova nepotpunost je karakteristična za sve jednadžbe gibanja fluida. Uzmemo li u obzir moment brzine razvoj polja brzine se može odrediti, a rezultat je jednadžba održanja momenata:
∂(ρu)/∂ t + ∇(ρu) u + ∇p= 0
gdje je p tlak. Problem je opet isti, rješenje ove jednadžbe zahtjeva poznavanje razvoja tlaka p. On se može odrediti uzimanjem u obzir drugog momenta što vodi na jednadžbu održanja energije, ali njeno rješenje ponovo zahtjeva uzimanje u obzir trećeg momenta itd. Umjesto da se tako nastavi, u dinamici fluida postavlja se jednadžba stanja kao jednadžba zatvaranja. Za nestlačive i neviskozne fluide kao treća jednadžba se dodaje:
∇u = 0
pa ove tri jednadžbe čine Eulerove jednadžbe za nestlačive i neviskozne fluide. Uzme li se u obzir molekularna viskoznost μ, ali i dalje uz pretpostavku nestlačivih homogenih fluida rezultat su Navier – Stokesove jednadžbe:
∂u /∂ t = – u ∇u – (1/ρ) ∇p + (μ/ρ)∇2u + (1/ρ) f
∇u = 0
gdje f pretstavlja sve druge sile kao što su gravitacija ili centrifugalne sile.
Navier – Stokesove jednadžbe su u osnovi temelj fizikalnih modela. Gore su navedene pojednostavljene jednadžbe za specifične uvjete nestlačivih homogenih fluida, a u stvarnim fizikalnim simulacijskim modelima širenja požara uključuju se i svojstva uzgona toplog zraka, konvekcije i turbulencija, pa se NS jednadžbe na odgovarajući način trebaju preformulirati.
Osim toga važni mehanizmi kod širenja požara su prijenos topline radijacijom, prijenos požara čvrstim česticama koji vjetar prenosi na područja koja nisu zapaljena (tzv. spotfires), interakcija požara s atmosferom i utjecaj topologije terena na širenje požara (ubrzano širenje požara na padinama).
Različiti modeli uključuju u većoj ili manjoj mjeri ove različite mehanizme. Neki od primjera postojećih fizikalnih modela koji su radovima dokumentirani su:
• AILOS-F – CINAR S.A. Grčka, 1994, 3D model, autor Crobe et al.,
• FIRETEC – Los Alamos National Laboratory, USA, 1997., 3D model, autor Linn
• Grishinov model - Tomsk State University, Rusija, 1997., 2D model, autor Grishin
• IUSTI – Institut Universitaire des Systemes Thermiques Industriels, Francuska, 1998., 2D model, autor Larin et al.,
• PIF97 – EFAISTOS projekt, Francuska, 1999., 2D model, autor Dupuy et al.,
• LEMTA – Laboratoire d'Energetique et de Mecanique Theorique et Appliquee, Francuska, 2002., 2(3)D model, autor Sero-Guillaume et al.,
• UoS – University of Salamance, Španjolska, 2002., 2D model, autor Asensio et al., i
• WFDS – National Institute of Safety Technology, USA, 2006, 3D model, autor Mell et al.,
a primjeri kvazi-fizikalnih modela su:
• ADFA I – Australian Defence Force Academy, Australia, 1989., 1D model, autor de Mestre
• TRW – USA, 1991., 2D model, autor Carter,
• Albinijev model – USA, 1996., 2D model, autor Albini,
• UC – University of Corsica, Francuska, 1998., 2D model, autor Santoni,
• ADFA II – Australia/USA, 1998., 2D model, autor Catchpole, i
• Coimbra model – Portugal, 2004., 2D model, autor Vaz et.al.
Kvazi-fizikalni modeli zahtijevaju određeno „a priori“ znanje o karakteristikama plamena i ne uključuju kemijske reakcije. Kod svih fizikalnih i kvazi-fizikalnih modela temeljni zakoni su uvijek isti, a modeli se uglavnom po metodologiji i načinu njihove implementacije ili po tome čemu su namijenjeni, da li predviđeno da se koriste u operativnom radu, eksperimentalnim istraživanjima ili imaju ulogu samo u akademskom obrazovanje. Neki od modela su toliko kompleksni, da nisu primjenjivi niti na analizu pojava kod kojih se reducira dimenzionalnost. Od modela koji su namijenjeni modeliranju širenja požara na prirodnoj skali posebno se ističu AILOS-F, FIRETEC, PIF97 i WFDS, međutim svi su oni izuzetno računski zahtjevni pa se često smanjuje rezolucija proračunske domene ili preciznost izračuna.
Primjer izlaznog ekrana različitih fizikalnih i kvazi-fizikalnih modela prikazuju slike 2.3.1 i 2.3.2.
Slika 2.3.1 Modeliranje širenja požara fizikalnim modelom FIRETEC (Los Alamos National Laboratory, USA)

Slika 2.3.2 Modeliranje širenja požara fizikalnim modelom WFDS (National Institute of Safety Technology, USA). Eksperimantalno goreje na probnom poligonu i rezultati simulacije korištenjem modela WFDS
Poseban problem kod fizikalnih modela su ulazni parametri i granični uvjeti koji znatno otežavaju usporedbu sa stvarnim širenjima požara, pogotovo u prirodnom okolišu. Zbog toga se najčešće provjeravaju u laboratorijskim uvjetima gdje se mogu osigurati kontrolirani uvjeti. Nedostatak su i računalni zahtjevi, koji su takvi da uvelike ograničavaju širu upotrebu, pogotovo u realnom vremenu. Na primjer za model WFDS proračun za područje veličine 1.5 km x 1.5 km x 0.2 km u rezoluciji 1.5x1.5x1.4 m i simulacijsko vrijeme od 100 sekundi na računalu sa velikom računalu sa 11 procesorskih čvorova traje čak 25 sati. Prema tome teško je očekivati da će se u slijedećem periodu ovakvi tipovi modela šire koristiti u operativnoj praksi, pa ih zbog toga u nastavku više niti ne razmatramo.